Actualizado a: 19 de diciembre de 2023
La industria de los chips semiconductores es muy compleja, las fábricas son un misterio para muchos, y en la información vemos conceptos extraños para muchos como el yield, binning, bkm, pero existen algunas leyes y fórmulas que te pueden ayudar a entenderla mejor, y en las que se basan muchos chips de procesamiento, memorias, etc., para seguir avanzando y obteniendo más rendimiento, o para determinar los límites de estos. Estos diminutos dispositivos electrónicos son la columna vertebral de innumerables aplicaciones de nuestra era, por eso, te animamos a conocer estas leyes fundamentales con este artículo donde exploraremos todo lo que debes saber sobre estos conceptos.
Ley de Moore
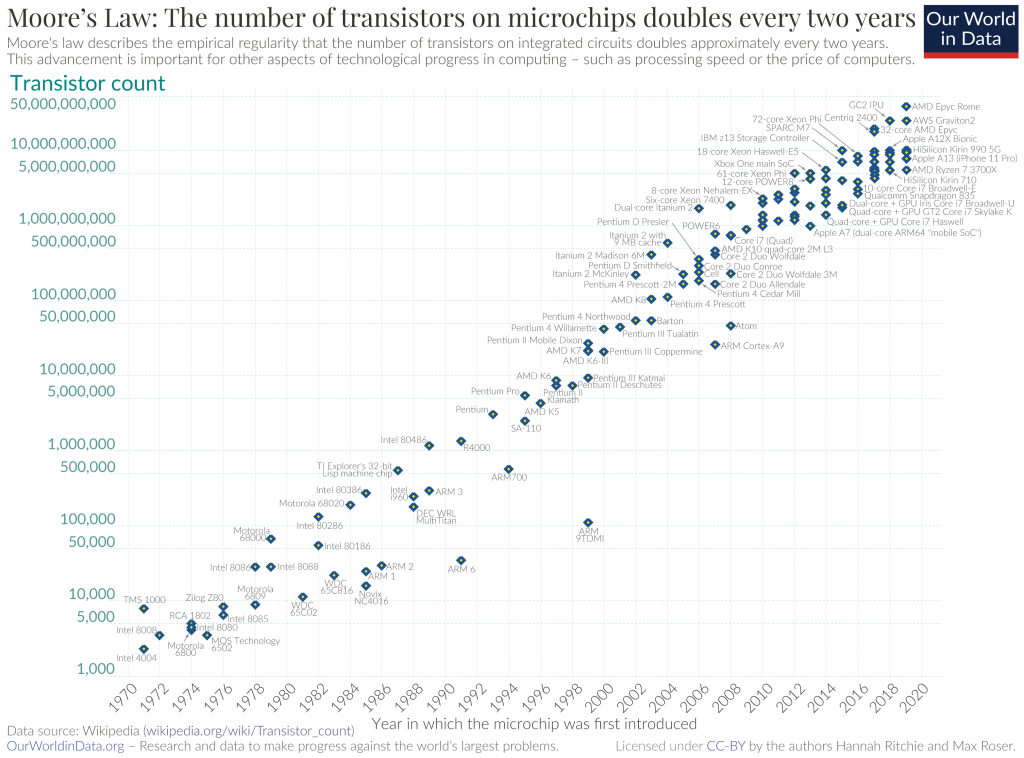
La Ley de Moore es la observación de que el número de transistores en un circuito integrado (CI) se duplica aproximadamente cada dos años. Esta observación, nombrada en honor a Gordon Moore, co-fundador de Fairchild Semiconductor e Intel, no es una ley física, sino una relación empírica vinculada a ganancias derivadas de la experiencia en producción.
Como curiosidad, decir que en un un artículo científico de 2005 titulado «Ley de Kryder», se describió cómo la densidad de almacenamiento de datos por unidad de superficie en los discos duros magnéticos estaba aumentando a una tasa que superaba la Ley de Moore.
Moore predijo inicialmente un duplicado anual en 1965, luego se ajustó a cada 18 meses, pero en 1975 ajustó la proyección a un duplicado cada dos años. Aunque la predicción inicial carecía de evidencia empírica, se ha mantenido desde 1975, convirtiéndose en una «ley». Esta predicción ha guiado la planificación a largo plazo en la industria de semiconductores y ha influido en avances clave en la electrónica digital, vinculándose a cambios tecnológicos, sociales y de crecimiento económico.
Sin consenso sobre su final, algunos informan que el avance de semiconductores se ha desacelerado desde 2010, desafiando ligeramente la predicción de Moore y alegando que está muerta, como el caso de Jensen Huang de Nvidia, en 2022. Sin embargo, otros aún siguen sosteniendo que está viva, como el caso de Pat Gelsinger de Intel. Los expertos están muy divididos, y eso no solo se ve en la teoría, también en la práctica.
Las tendencias recientes en la ingeniería de transistores a escala nanométrica muestran avances significativos en el diseño de puertas para controlar el flujo de corriente en canales delgados. Los transistores nanométricos, como el FinFET y el GAAFET, han surgido como soluciones comunes para abordar los desafíos de controlar la corriente en canales cada vez más delgados frente a los tradicionales MOSFET planar. Desde la demostración del GAAFET en 1988 hasta la fabricación de chips de 2 nm anunciada por IBM en mayo de 2021, la industria ha experimentado avances notables.
También se han explorado enfoques alternativos, como la lógica y memoria basadas en el estado de giro del electrón (spintronics) y materiales avanzados para canales de nanoalambre. La investigación con materiales no tradicionales, como el arseniuro de indio y galio (InGaAs), ha demostrado promesas para futuras aplicaciones de lógica de alta velocidad y bajo consumo de energía. Además, se ha explorado el uso de grafeno en la electrónica, aunque se requiere más investigación, especialmente para capas de grafeno menores a 50 nm. Sin embargo, estas alternativas no han calado, ya sea porque aún necesitan desarrollo o porque no aportan soluciones mucho mejores que el actual silicio.
Ley de Rock o 2ª Ley de Moore
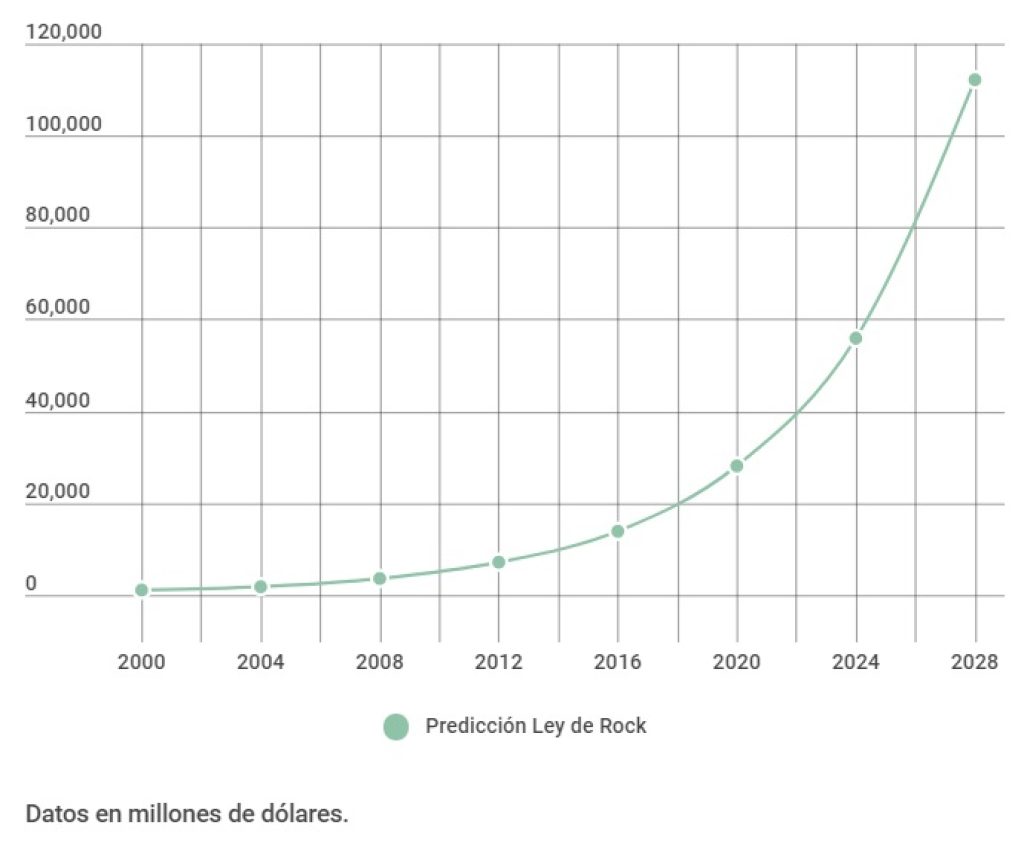
La Ley de Rock, también conocida como la Segunda Ley de Moore y nombrada en honor a Arthur Rock, establece que el costo de una planta de fabricación de chips semiconductores se duplica cada cuatro años. Hasta 2015, el precio ya había alcanzado aproximadamente 14 mil millones de dólares.
Esta ley puede entenderse como la contraparte económica de la Ley de Moore (primera ley) que establece que el número de transistores en un circuito integrado denso se duplica cada dos años. La segunda ley de Moore es una consecuencia directa del crecimiento continuo de la industria de semiconductores, que es intensiva en capital. Productos innovadores y populares generan más ganancias, lo que significa más capital disponible para invertir en niveles cada vez más altos de integración a gran escala. Esto, a su vez, conduce a la creación de productos aún más innovadores.
La industria de semiconductores siempre ha sido extremadamente intensiva en capital, con costes de fabricación de cada unidad disminuyen constantemente. Por lo tanto, los límites finales para el crecimiento de la industria limitarán la cantidad máxima de capital que se puede invertir en nuevos productos. En algún momento, la Ley de Rock chocará con la Ley de Moore.
Se ha sugerido que los costes de las plantas de fabricación no han aumentado tan rápidamente como predice la Ley de Rock, llegando a una meseta a finales de la década de 1990. También se plantea la idea de que el costo de la planta de fabricación por transistor, que ha mostrado una tendencia pronunciada a la baja, puede ser más relevante como restricción para la Ley de Moore.
Ley de Gustavson
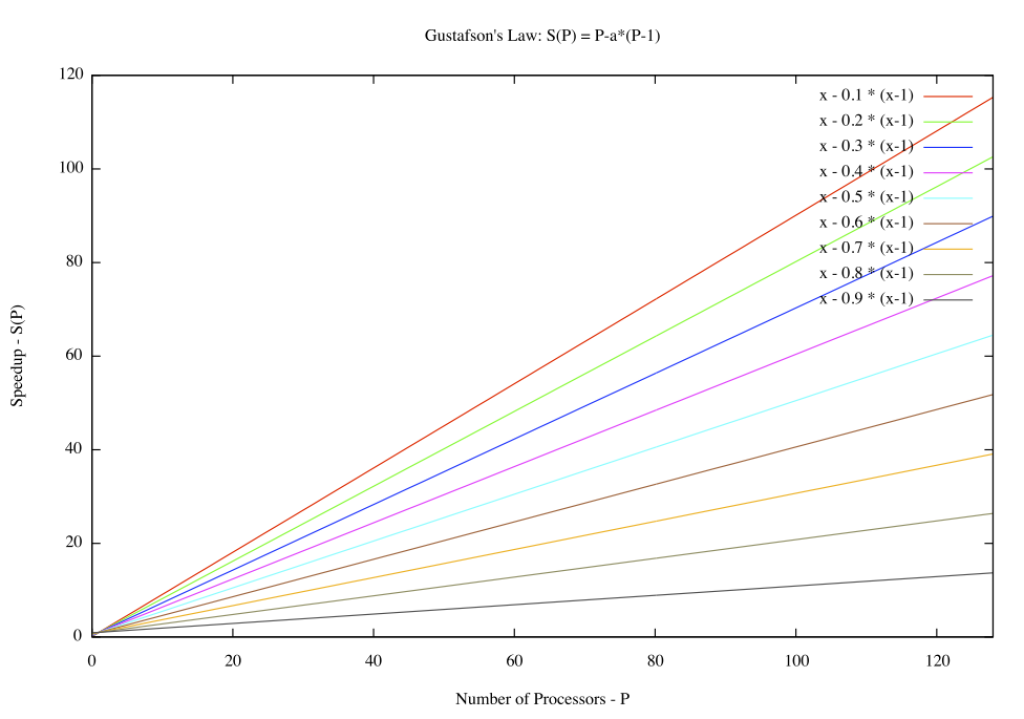
La Ley de Gustafson (también conocida como Ley de Gustafson-Barsis) proporciona una medida del aumento de velocidad en el tiempo de ejecución de una tarea que teóricamente se beneficia de la computación paralela, utilizando una ejecución hipotética de la tarea en una máquina de un solo núcleo como referencia. En otras palabras, representa la «ralentización» teórica de una tarea que ya está paralelizada si se ejecuta en una máquina serial. Esta ley lleva el nombre del científico de la computación John L. Gustafson y su colega Edwin H. Barsis, y se presentó en el artículo «Reevaluating Amdahl’s Law» en 1988.
Para comprender mejor la Ley de Gustafson, es crucial considerar el contexto de las tendencias en computación paralela. A diferencia de la Ley de Amdahl, que se centra en el límite de mejora de la velocidad debido a la porción secuencial de un programa, la Ley de Gustafson asume que, a medida que se aumenta el tamaño del problema, también se aumenta la cantidad de trabajo paralelizable. En lugar de considerar una fracción fija de trabajo secuencial, la Ley de Gustafson sugiere que, en problemas más grandes, la porción paralelizable puede aumentar, lo que permite una mejora continua en la velocidad de ejecución a medida que se añaden más recursos computacionales.
La formulación matemática de la Ley de Gustafson implica una relación directa entre el tamaño del problema y el grado de paralelismo posible. A medida que el tamaño del problema aumenta, la porción paralelizable también aumenta, lo que resulta en un mayor rendimiento general del sistema. Esta perspectiva más optimista respecto a la computación paralela destaca la importancia de considerar no solo la eficiencia de la paralelización en sí, sino también cómo esta eficiencia puede escalar con el tamaño del problema.
Ley de Amdahl
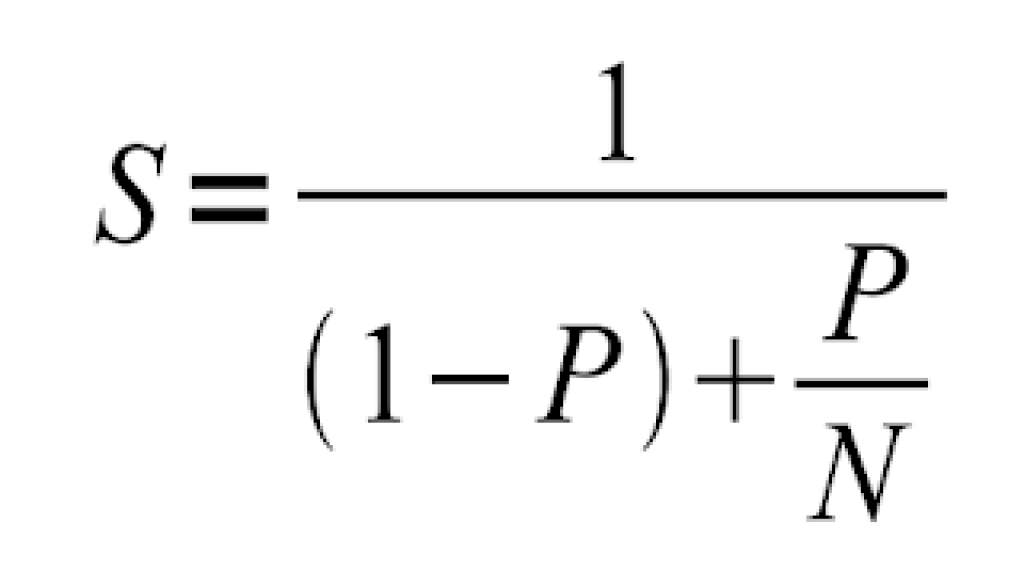
El argumento o Ley de Amdahl (llamada así por el informático Gene Amdahl, que la presentó por primera vez en la conferencia AFIPS de 1967) es una fórmula que proporciona el aumento teórico de velocidad en la latencia de la ejecución de una tarea con una carga de trabajo fija que se puede esperar de un sistema cuyos recursos se mejoran. La ley establece que «la mejora de rendimiento general obtenida al optimizar una parte única de un sistema está limitada por la fracción de tiempo que la parte mejorada se utiliza realmente«.
Para comprender en profundidad la Ley de Amdahl, es esencial considerar su aplicación en el contexto de la mejora del rendimiento de sistemas computacionales. La ley destaca la importancia de identificar y optimizar las partes críticas de un sistema para obtener mejoras significativas en el rendimiento general. La fórmula asociada a la Ley de Amdahl se expresa como una relación entre la fracción del tiempo que se mejora una parte específica del sistema y la mejora total de rendimiento que se puede lograr.
La contribución principal de la Ley de Amdahl radica en su énfasis en la optimización equilibrada de todas las partes críticas de un sistema. En otras palabras, aunque mejorar una parte del sistema puede tener beneficios significativos, la ley advierte que el impacto general estará limitado por la fracción de tiempo que dicha parte mejorada realmente se utiliza durante la ejecución de la tarea.
Esta limitación inherente resalta la importancia de un enfoque holístico para la mejora del rendimiento del sistema, donde se considere cuidadosamente cada componente y su contribución relativa al tiempo total de ejecución. La Ley de Amdahl se ha vuelto fundamental en la planificación y diseño de sistemas informáticos, ya que proporciona una guía valiosa para maximizar la eficiencia y el rendimiento en la búsqueda de mejoras tecnológicas. En resumen, la Ley de Amdahl subraya la necesidad de abordar de manera integral las limitaciones temporales específicas de cada componente para lograr mejoras de rendimiento significativas en sistemas informáticos.
Por ejemplo, aplicando la fórmula anterior, donde S es la aceleración que se puede alcanzar a partir de modificaciones o mejoras de la arquitectura y P es la porción de cálculo, mientras que N es el número de procesadores. Entonces, podemos imaginar que si queremos mejorar un 30% el tiempo de ejecución, entonces se debería ajustar la fórmula para S= 0.3.
Ley de Koomey
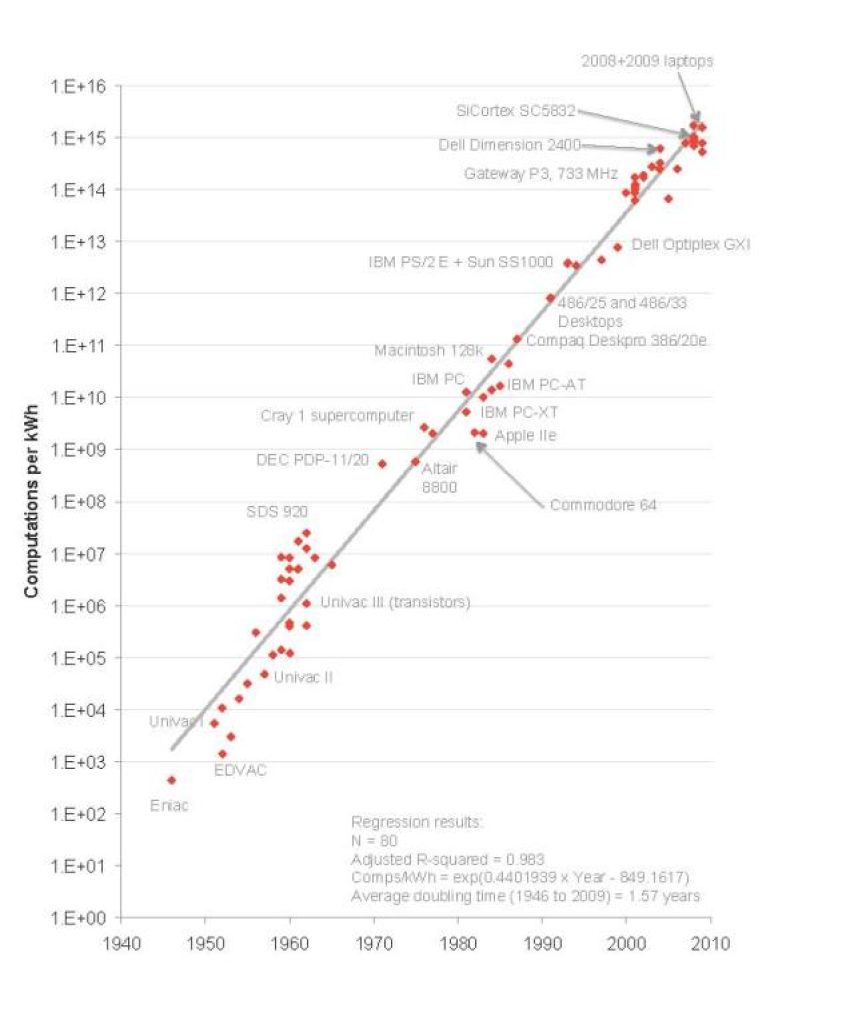
La Ley de Koomey describe una tendencia en la historia del hardware informático: durante aproximadamente medio siglo, el número de cálculos por julio de energía disipada se duplicó aproximadamente cada 1.57 años. El profesor Jonathan Koomey describió esta tendencia en un artículo de 2010, donde afirmó que «a una carga informática fija, la cantidad de batería que necesitas disminuirá a la mitad cada año y medio«.
Esta tendencia fue notablemente estable desde la década de 1950 (con un R2 superior al 98%). Sin embargo, en 2011, Koomey volvió a examinar estos datos y encontró que después del año 2000, la duplicación se ralentizó a aproximadamente una vez cada 2.6 años. Esto está relacionado con la desaceleración de la Ley de Moore, la capacidad de construir transistores más pequeños, y el fin, alrededor de 2005, de la escala de Dennard, la capacidad de construir transistores más pequeños con densidad de potencia constante.
Koomey señaló que la diferencia entre estas dos tasas de crecimiento es significativa. Una duplicación cada año y medio resulta en un aumento de eficiencia de 100 veces cada década, mientras que una duplicación cada dos años y medio solo produce un aumento de 16 veces.
Las implicaciones de la Ley de Koomey cobran fuerza a medida que los dispositivos informáticos se vuelven más pequeños, como los dispositivos móviles, esta tendencia puede ser aún más importante que las mejoras en la potencia de procesamiento bruta para muchas aplicaciones. Además, los costes de energía se están volviendo un factor cada vez más importante en la economía de los centros de datos, lo que aumenta la importancia de la Ley de Koomey.
La desaceleración de la Ley de Koomey tiene implicaciones para el uso de energía en la tecnología de la información y las comunicaciones. Sin embargo, debido a que las computadoras no funcionan continuamente a su máxima potencia, los efectos de esta desaceleración pueden no ser evidentes durante una década o más. Koomey advierte que, como con cualquier tendencia exponencial, esta eventualmente llegará a su fin. En una década aproximadamente, el consumo de energía volverá a estar dominado por la potencia consumida cuando una computadora está activa, y esta potencia activa seguirá estando sujeta a la física detrás de la desaceleración de la Ley de Moore.
Escala Dennard
La escala de Dennard, también conocida como la escala de MOSFET, es una ley de escalamiento que afirma que, a medida que los transistores se hacen más pequeños, su densidad de potencia se mantiene constante, de modo que el uso de energía se mantiene proporcional al área; tanto el voltaje como la corriente se escalan hacia abajo con la longitud. La ley, originalmente formulada para MOSFET, se basa en un artículo de 1974 coescrito por Robert H. Dennard, de IBM, de quien toma su nombre.
El modelo de escala de MOSFET de Dennard implica que, con cada generación tecnológica:
- Las dimensiones del transistor podrían escalar en un -30% (0.7×). Esto tiene efectos simultáneos: la área de un dispositivo individual se reduce en un 50%, porque el área es longitud por ancho. La capacitancia asociada al dispositivo, C, se reduce en un 30% (0.7×), porque la capacitancia varía con el área sobre la distancia. Para mantener el campo eléctrico inalterado, el voltaje, V, se reduce en un 30% (0.7×), porque el voltaje es el campo por la longitud. Características como la corriente y el tiempo de transición también se reducen en un 30%, debido a su relación con la capacitancia y el voltaje. Se asume que la demora general del circuito está dominada por el tiempo de transición, por lo que también se reduce en un 30%.
- Estos efectos conducen a un aumento en la frecuencia de operación, f, de aproximadamente un 40% (1.4×), porque la frecuencia varía con el inverso de la demora.
- El consumo de energía de un transistor individual disminuye en un 50%, porque la potencia activa es P=C·V²·f, siendo C la capacitancia, V el voltaje al que trabaja el chip, y f la frecuencia de reloj.
Por lo tanto, en cada generación tecnológica, la área y el consumo de energía de los transistores individuales se reducen a la mitad. En otras palabras, si la densidad de transistores se duplica, el consumo de energía (con el doble de transistores) permanece igual.
Relacionado con la Ley de Moore y el rendimiento, la Ley de Moore dice que el número de transistores se duplica aproximadamente cada dos años. Combinado con la escala de Dennard, esto significa que el rendimiento por julio de energía crece aún más rápido, duplicándose aproximadamente cada 18 meses. Esto a veces se denomina la Ley de Koomey. El ritmo de duplicación fue sugerido originalmente por Koomey como 1.57 años, pero estimaciones más recientes sugieren que se está desacelerando.
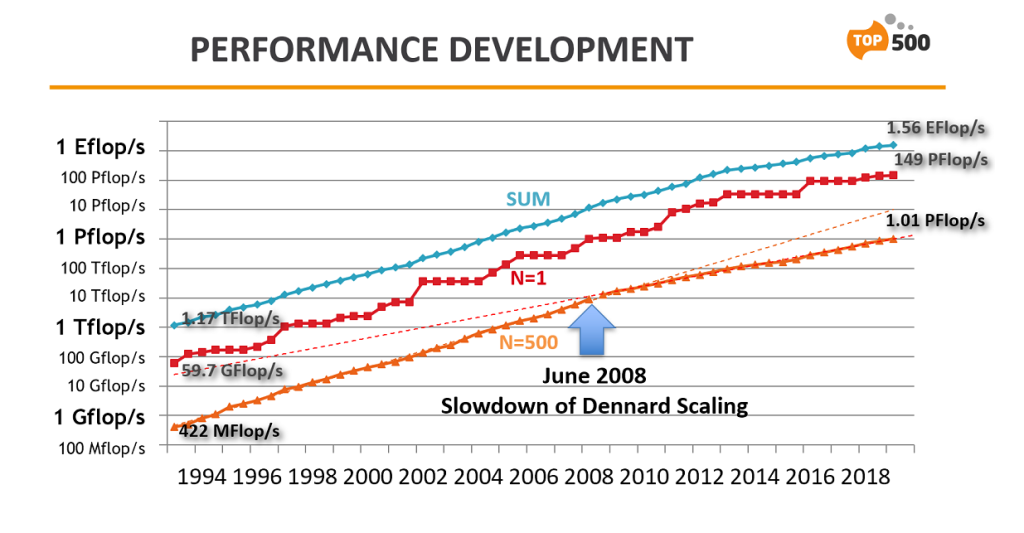
Alrededor de 2006 la escala Dennard se quiebra, deja de ser efectiva. Esto se atribuye al aumento de la fuga de corriente a tamaños pequeños, lo que plantea mayores desafíos y provoca un aumento en la temperatura del chip, amenazando con un aumento adicional en los costos de energía. Esto ha llevado a los fabricantes de CPU a centrarse en procesadores multinúcleo como una forma alternativa de mejorar el rendimiento, ya que el aumento en el número de núcleos beneficia a muchas cargas de trabajo, pero también conlleva un aumento en el consumo de energía general. La descomposición de la escala de Dennard ha llevado a la limitación de la frecuencia del reloj y ha obligado a considerar nuevas estrategias para gestionar la disipación de energía, como el concepto de «silicio oscuro«, que se refiere al área inactiva de un circuito integrado debido a restricciones de potencia.
Límite de Bremermann

El límite de Bremermann es una medida teórica que establece la velocidad máxima a la que un sistema autónomo en el universo material puede realizar cálculos. Se basa en principios fundamentales de la física cuántica y la relación masa-energía de Einstein. La fórmula asociada a este límite es mc2/h, que se traduce en aproximadamente 1.3563925 · 1050 bits por segundo por kilogramo. Como sabrás de la fórmula de F=mc2 de Einstein, m es la masa en gramos, c es la velocidad de la luz.
Este límite tiene implicaciones prácticas en criptografía, ya que puede utilizarse para determinar el tamaño mínimo de claves de cifrado o valores hash necesarios para crear un algoritmo que sería extremadamente difícil de descifrar mediante métodos de fuerza bruta. Por ejemplo, si imaginamos una computadora con la masa de toda la Tierra operando en este límite, podría realizar alrededor de 1075 operaciones matemáticas por segundo. Esto tiene implicaciones en la seguridad de las claves criptográficas, ya que claves más largas aumentan significativamente el tiempo necesario para descifrar la información, haciendo que sea más segura.
Bekenstein bound
La Bekenstein bound, descrita por Jacob Bekenstein, es un límite superior para la entropía termodinámica (S) o la entropía de Shannon (H) que puede contenerse dentro de una región finita de espacio que tiene una cantidad finita de energía, o viceversa, la cantidad máxima de información necesaria para describir perfectamente un sistema físico dado hasta el nivel cuántico. Implica que la información de un sistema físico, o la información necesaria para describir perfectamente ese sistema, debe ser finita si la región de espacio y la energía son finitas. En el ámbito de la informática, esto sugiere que modelos no finitos como las máquinas de Turing no son realizables como dispositivos finitos.
Este concepto proviene de la interrelación entre la información y la energía en la mecánica cuántica y establece un límite teórico en la cantidad de información que puede existir en una región del espacio físico. Esencialmente, nos dice que hay un tope máximo para la cantidad de información que podemos tener sobre un sistema físico en función de la energía y el espacio disponibles. Esto tiene implicaciones profundas para la teoría de la información y la capacidad de procesamiento de la información en sistemas físicos limitados. En términos prácticos, la Bekenstein bound nos dice que hay un límite fundamental para la descripción detallada de sistemas físicos finitos, incluso a nivel cuántico, y nos brinda una comprensión más profunda de la relación entre la información, la energía y el espacio en el universo.
Teoremas de los límites de la velocidad cuántica
En la mecánica cuántica, existen dos teoremas fundamentales relacionados con el límite de velocidad cuántica: el Teorema de No Comunicación y el Teorema de Velocidad Cuántica Máxima. El Teorema de No Comunicación establece que no es posible transmitir información instantáneamente entre dos sistemas cuánticos distantes. Incluso cuando dos partículas cuánticas están entrelazadas de manera que el estado de una está correlacionado con el estado de la otra, cualquier cambio realizado en una partícula no puede influir instantáneamente en la otra, manteniendo así la velocidad máxima de transmisión de información establecida por la velocidad de la luz, algo de lo que ya hablamos en este otro artículo sobre la superluminal computing.
Por otro lado, el Teorema de Velocidad Cuántica Máxima, derivado de la teoría de la relatividad, sostiene que ninguna partícula o información puede viajar más rápido que la velocidad de la luz en el vacío. Este límite impuesto por la velocidad de la luz establece una barrera infranqueable para la propagación de información y eventos en el espacio-tiempo. Ambos teoremas son esenciales para comprender las limitaciones fundamentales impuestas por la teoría cuántica y la relatividad en la transmisión de información y cambios cuánticos en el universo.
Principio de Landauer
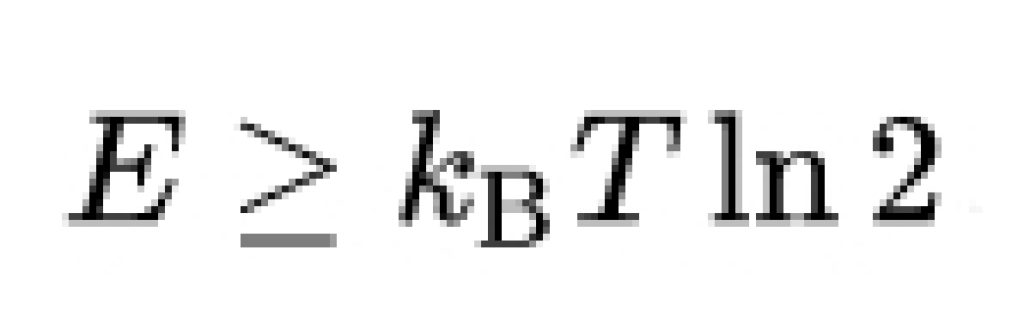
El principio de Landauer es un principio físico que se refiere al límite teórico inferior del consumo de energía en informática. Este principio sostiene que un cambio irreversible en la información almacenada en un ordenador, como la fusión de dos caminos computacionales, disipa una cantidad mínima de calor hacia su entorno.
Este principio fue propuesto por Rolf Landauer en 1961. Gracias a él se puede establecer que la energía mínima necesaria para borrar un bit de información es proporcional a la temperatura a la que opera el sistema, expresada como puedes ver en la imagen superior, donde kB es la constante de Boltzmann. A temperatura ambiente, el límite de Landauer representa una energía de aproximadamente 0.018 eV. Aunque los ordenadores modernas utilizan alrededor de mil millones de veces más energía por operación, los experimentos físicos han confirmado las predicciones del principio de Landauer. Sin embargo, el principio ha sido cuestionado en los últimos años debido a posibles fallos en el razonamiento circular y suposiciones defectuosas, aunque también se ha defendido como una ley física válida.
Ley de Huang
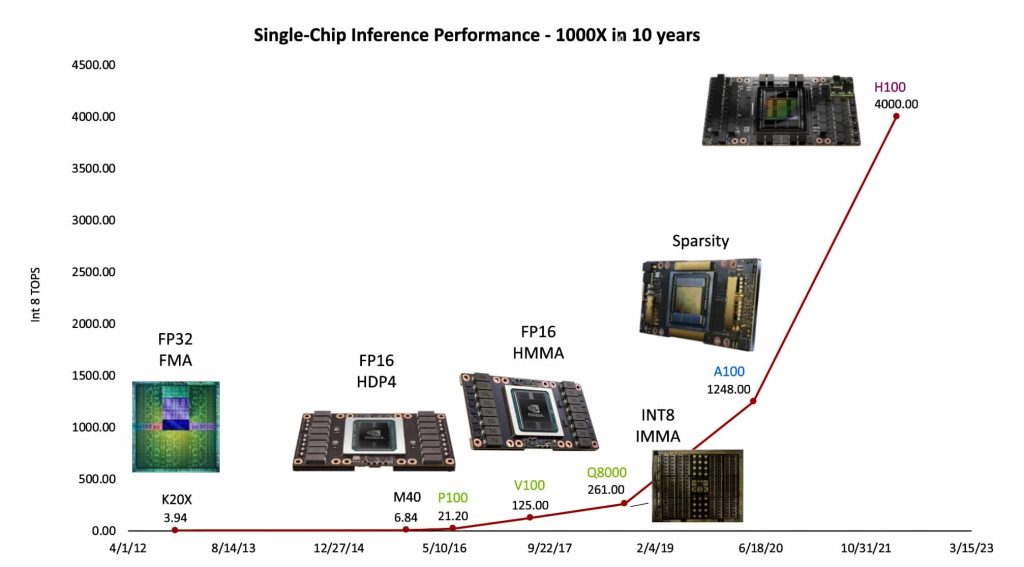
La Ley de Huang es una observación en informática e ingeniería que señala que los avances en las unidades de procesamiento gráfico (GPU) están creciendo a una tasa mucho más rápida que las unidades centrales de procesamiento (CPU) tradicionales. A diferencia de la Ley de Moore, que predice que el número de transistores en un circuito integrado denso se duplica aproximadamente cada dos años, la Ley de Huang establece que el rendimiento de las GPU supera la duplicación cada dos años.
Esta observación fue hecha por Jensen Huang, CEO de Nvidia, en 2018, quien destacó que las GPU de Nvidia eran «25 veces más rápidas que hace cinco años«, superando la expectativa de la Ley de Moore (la que cree que está muerta, como dije anteriormente) de un aumento de diez veces en ese período. Según Huang, la sinergia entre hardware, software e inteligencia artificial hace posible esta nueva ley. Aunque ha recibido críticas y algunas cuestionamientos sobre su validez, la Ley de Huang destaca la importancia de la innovación en toda la pila tecnológica y no solo en los chips, especialmente en el contexto de la inteligencia artificial y el aprendizaje profundo.
Ley de Grosch
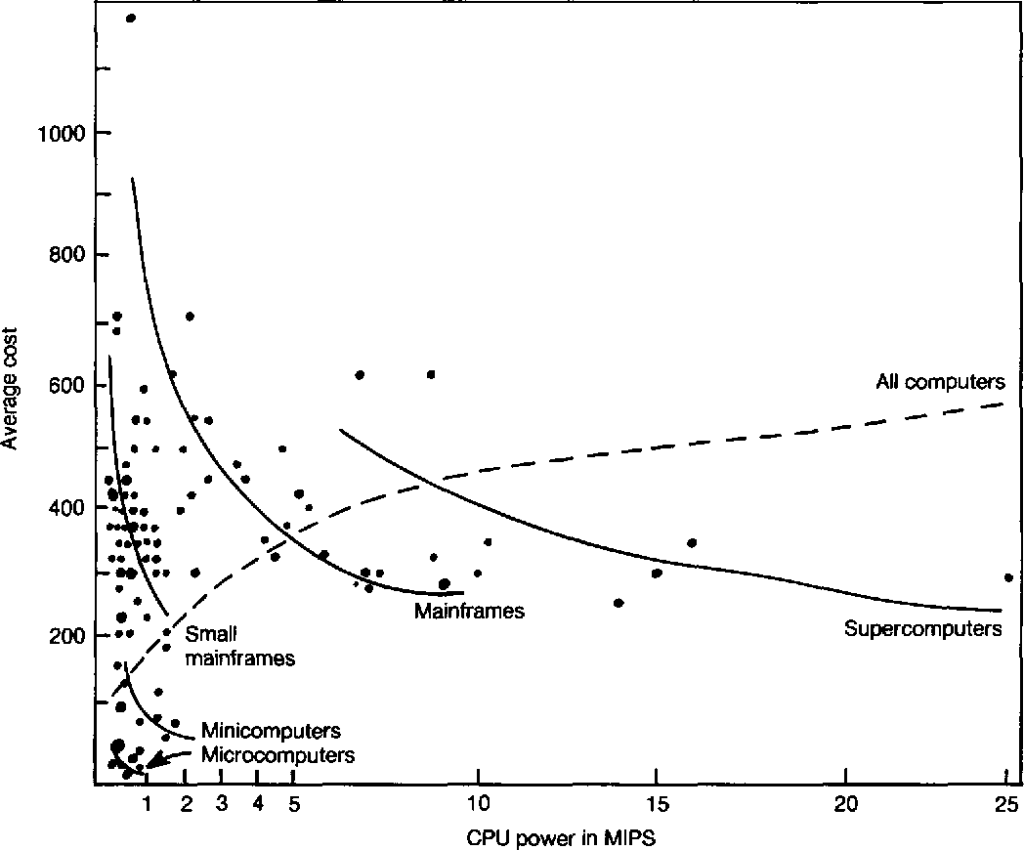
La ley de Grosch es una observación sobre el rendimiento de los ordenadores realizada por Herb Grosch en 1953. Se expresa como una regla fundamental que proporciona una economía adicional solo en función de la raíz cuadrada del aumento de velocidad. En otras palabras, para realizar un cálculo diez veces más económico, se debe hacer cien veces más rápido.
Esta máxima se formula más comúnmente como «el rendimiento del ordenador aumenta como el cuadrado del coste«. Si un ordenador A cuesta el doble que un ordenador B, se espera que el ordenador A sea cuatro veces más rápido que B.
Grosch sugirió que los ordenadores presentan economías de escala, lo que significa que cuanto más costosa seael ordenador, mejor será la relación precio-rendimiento de manera lineal. Sin embargo, este enfoque puede implicar que los ordenadores de bajo coste no pueden competir en el mercado, algo que no es cierto. Los análisis modernos ya no sugieren esto, y algunos como Paul Strassmann apuntan a que la Ley de Grosch tansolo reflejaba los precios a los que IBM vendía sus equipos entre 1960 y 1970.
Otras leyes
A parde las anteriores, también existen otras leyes que tienen que ver con los ordenadores de un modo u otro, aunque no estén tan relacionados con los semiconductores o chips:
Ley de Wirth
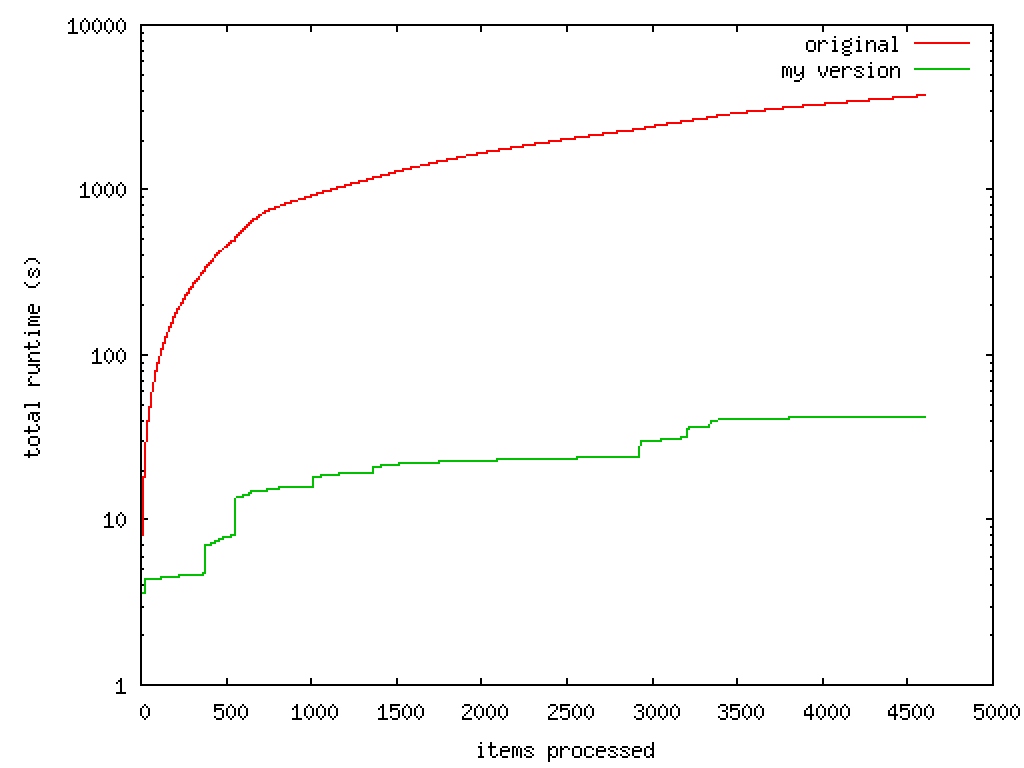
La Ley de Wirth versa sobre el rendimiento de lordenadores, y afirma que el software se está volviendo más lento más rápidamente de lo que el hardware está mejorando en velocidad. Algo que indica la necesidad de optimizar el software y hacerlo más sencillo para hacer la misma tarea, como la filosofía Unix. Así lo describió Niklaus Wirth en 1997, en uno de sus artículos publicados.
Ley de Neven
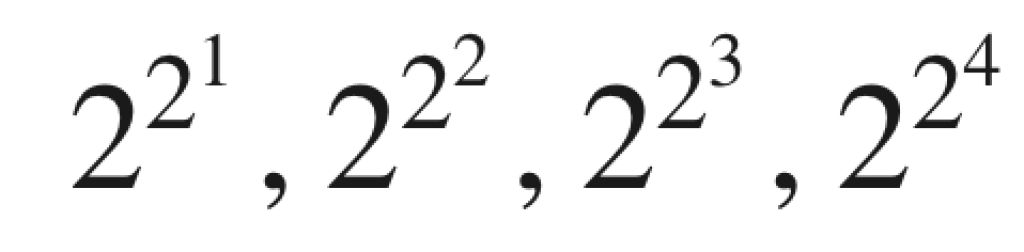
Hartmut Neven hizo una observación de que los ordenadores cuánticas están ganando poder computacional a una tasa doblemente exponencial. Esto es lo que se conoce como Ley de Neven. Algunos la conocen como la Ley de Moore de la computación cuántica.
Ley de Bell
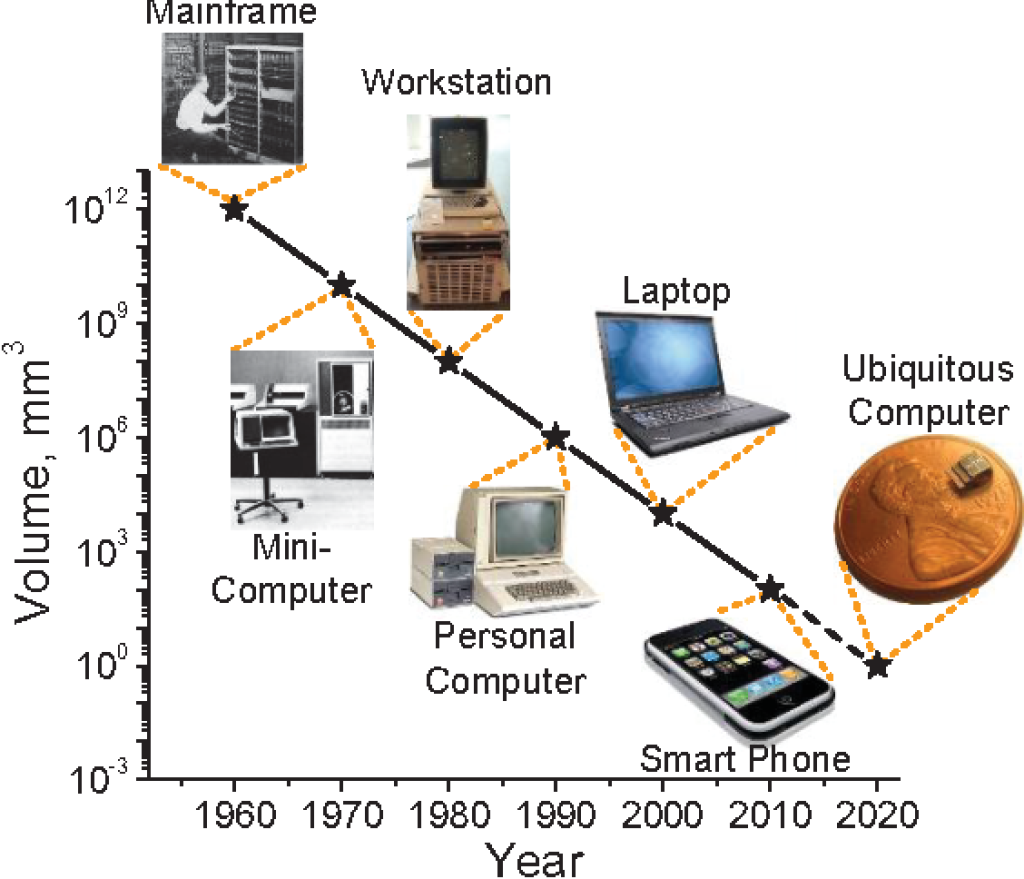
La Ley de Bell, formulada por Gordon Bell en 1972, describe cómo los tipos de sistemas informáticos (o clases de ordenadores) se forman, evolucionan y eventualmente pueden extinguirse. Bell considera esta ley como parcialmente una corolario de la ley de Moore, que establece que «el número de transistores por chip se duplica cada 18 meses«. A diferencia de la ley de Moore, una nueva clase de ordenadores generalmente se basa en componentes de menor costo que tienen menos transistores o menos bits en una superficie magnética, etc. Se forma una nueva clase aproximadamente cada década, y lleva hasta una década comprender cómo se formó, evolucionó y es probable que continúe.
Una vez formada, una clase de menor precio puede evolucionar en rendimiento para tomar el control y perturbar una clase existente. Esta evolución ha llevado a la formación de grupos de ordenadores personales escalables con un rango de precio y rendimiento que va desde un PC hasta mainframes.
Ley de escalamiento neural
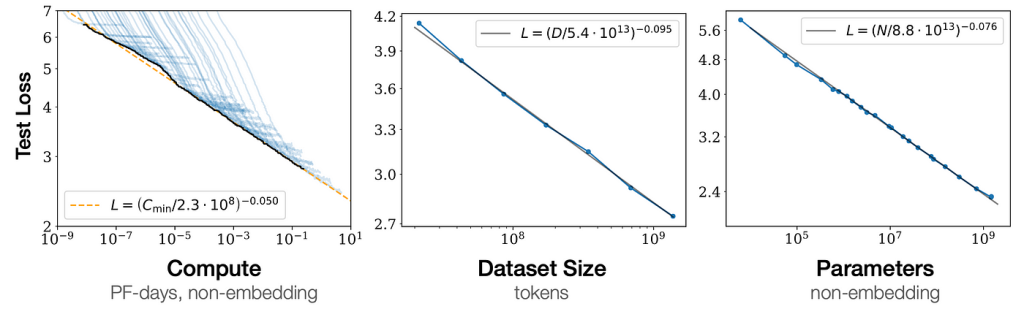
En aprendizaje automático, la ley de escalamiento neural relaciona parámetros de una familia de redes neuronales. Esta familia de modelos neuronales puede caracterizarse por cuatro parámetros: el tamaño del modelo (número de parámetros), el tamaño del conjunto de datos de entrenamiento, el costo del entrenamiento y el rendimiento después del entrenamiento. Estos parámetros están empíricamente relacionados por leyes estadísticas simples llamadas «leyes de escalamiento». La notación comúnmente utilizada para estos parámetros es N (número de parámetros), D (tamaño del conjunto de datos), C (costo computacional) y L (pérdida).
El tamaño del modelo generalmente se refiere al número de parámetros en la red neuronal, pero en modelos dispersos, como los modelos de mezcla de expertos, donde solo se utilizan fracciones de los parámetros durante la inferencia, puede haber complicaciones. El tamaño del conjunto de datos de entrenamiento se mide por la cantidad de puntos de datos que contiene y, por lo general, se prefiere conjuntos de datos más grandes ya que proporcionan una fuente más rica y diversa de información para que el modelo aprenda. Sin embargo, un conjunto de datos más grande también implica mayores recursos computacionales y tiempo para el entrenamiento del modelo.
El coste del entrenamiento se mide en términos de tiempo y recursos computacionales, y puede reducirse significativamente mediante algoritmos de entrenamiento eficientes y hardware especializado como GPU o TPU o NPU. Este costo es una función de varios factores, incluido el tamaño del modelo, el tamaño del conjunto de datos, la complejidad del algoritmo de entrenamiento y los recursos computacionales disponibles.
Ley de Zimmermann

En 2013, un artículo titulado «Ley de Zimmermann» escrito por Phil Zimmermann, aseguraba que: «El flujo natural de la tecnología tiende a avanzar en la dirección de facilitar la vigilancia» y «la capacidad de las computadoras para rastrearnos se duplica cada dieciocho meses«, haciendo referencia a la Ley de Moore.
Efemeralización

La Efemerización es un término acuñado por R. Buckminster Fuller en 1938, se refiere a la capacidad del avance tecnológico para hacer «más y más con menos y menos hasta que eventualmente puedas hacer todo con nada«, es decir, un aumento acelerado en la eficiencia para lograr la misma o mayor producción (productos, servicios, información, etc.) con menos insumos (esfuerzo, tiempo, materiales, recursos, etc.).
La sustitución de los ordenadores que han hecho en muchos casos los dispositivos móviles es un caso de esta efemerización que explica Fuller, siguiendo con el progreso tecnológico, usando cada vez menos materiales. Sin embargo, algunos estudiosos como Francis Heylighen y Alvin Toffler plantean que, aunque la efemerización puede aumentar nuestra capacidad para resolver problemas físicos, también puede empeorar los problemas no físicos. La creciente complejidad del sistema y la sobrecarga de información pueden hacer que sea difícil y estresante para las personas controlar estos sistemas efemerizados.





