Como sabes, cuando se habla del rendimiento de una CPU o una GPU, seguro que has escuchado hablar de los números enteros y los de coma flotante. O tal vez también lo hayas visto en programación, según los tipos de datos aceptados por un lenguaje concreto. Sea como sea, muchos aún no saben qué son estos números, sus diferencias, usos, etc. Por eso, en este tutorial te lo explicaremos todo…
Quiás también te interese conocer:
- ¿Qué son los FLOPS?
Terminología
Antes de comenzar con la teoría sobre los enteros y el coma flotante, hay que tener presente algunos conceptos o vocabulario que vas a ver a lo largo de este artículo. Los términos que deberías conocer son:
- Tipos de datos: se refiere al tipo de representación de un dato según el formato, como puede ser un entero (integer), coma flotante (floating point), una cadena o string, etc. Además, pueden ser con signo, sin signo, etc. Y podrían estar representados en binario, en decimal, en hexadecimal, octal, etc.
- Longitud: la longitud de los datos se refiere a la cantidad de bits necesaria para su representación. Por ejemplo, pueden ser de 8-bit, es decir, que se podrían representar desde 00000000 a 11111111, que es el equivalente en decimal a representar desde 0 a 255 (256 valores posibles).
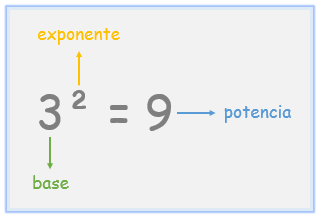
- Exponente: se trata de una forma de expresar una multiplicación de una expresión por sí misma un número determinado de veces.
- Base: en un número con exponente, se trata del número en sí al que se le aplica el exponente.
- Mantisa: es la sección de un número de coma flotante antes del lugar del decimal.
- Precisión: se refiere a qué tan preciso es un valor.
Enteros (integer)
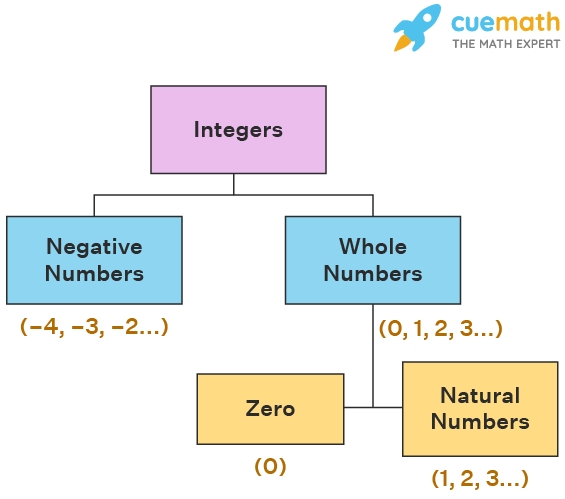
Los números enteros son aquellos que incluyen a los números positivos y los negativos, además del cero. La palabra «entero» es de procedencia latina y que indica que no son números con fracciones o decimales.
Definición de números enteros
Un número entero es un número sin parte decimal o fraccionaria e incluye números negativos y positivos, además del cero, que actúa como punto de partida para los otros dos. Además,m estos números se suelen representar en matemáticas con una Z:
Z= {… -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 5, 6, 7 …}
- Números positivos: un número es positivo si es mayor que cero. Por ejemplo, 1, 2, 3, etc. Estos números se suelen representar sin ningún símbolo o con un + delante.
- Números negativos: un número es negativo si es menor que cero. Ejemplo: -1, -2, -3 . . . Como ves, siempre deben tener el – delante (en código binario, se pueden usar el bit de signo).
- Cero: no se define como un número negativo ni como un número positivo. Es un número entero sin más, pero neutral. Además, como sabes, este número que tuvo su origen en el mundo árabe, y que fue transmitido desde la actual Andalucía hacia el resto de Europa, y es fundamental para los sistemas binarios en los que se basa la informática actual.
Operaciones con enteros
Cuando se trata de enteros, existen varias operaciones matemáticas de tipo aritmético que son fundamentales, como son:
- Suma: sumar enteros es el proceso de conseguir un resultado que sea la suma de dos o más de estos valores. Podría aumentar o disminuir, ya que si se están sumando números negativos actuarán como una resta, como deberías saber.
- Cuando ambos números enteros tienen el mismo signo, se suman sus valores absolutos. Por ejemplo: 1 + 2 = 3, -3 + (-2) = -5.
- Cuando los enteros son de diferente signo, entonces se deberá actuar como una resta, como he comentado, es decir, será la resta de los valores. Por ejemplo: 12 + (-1) = 11
- Resta: restar números enteros es el proceso de encontrar la diferencia entre dos o más números, y en este caso también puede resultar un aumento o una disminución dependiendo del signo. La resta también tiene sus reglas, como las de la suma. Por ejemplo, si queremos restar (+4) – (+3) = 1, en cambio, 4 – 7 = -3.
- Multiplicación: la multiplicación de enteros también usará varias reglas según l signo. Puedes ver la tabla de multiplicar más abajo para saber cuáles son estas reglas. Pero, para poner un ejemplo de multiplicación: 3 x 11 = 33, -2 x 1 = -2.
- División: para la división de números enteros también se sigue algo parecido, y creo que no hace falta explicarlo. También te dejo la tabla más abajo.
| Producto o multiplicación | Resultado | Ejemplo |
|---|---|---|
| (+) × (+) | + | 2 × 3 = 6 |
| (+) × (-) | – | 2 × (-3) = -6 |
| (-) × (+) | – | (-2) × 3 = -6 |
| (-) × (-) | + | (-2) × (-3) = 6 |
| División | Resultado | Ejemplo |
|---|---|---|
| (+) ÷ (+) | + | 12 ÷ 3 = 4 |
| (+) ÷ (-) | – | 12 ÷ (-3) = -4 |
| (-) ÷ (+) | – | (-12) ÷ 3 = -4 |
| (-) ÷ (-) | + | (-12) ÷ (-3) = 4 |
Cuando se trata de números enteros representados en binario, una CPU realizará estas operaciones aritméticas sencillas en las unidades de ejecución, como la ALU (Arithmetic Logic Unit) o unidades específicas de suma, multiplicación, etc. Además, como deberías saber, con estas operaciones elementales se pueden implementar otras operaciones…
En sistema digital
Sin embargo, hasta aquí hemos asumido que se trata de números decimales. Pero como sabes, en un ordenador se usan valores digitales, por lo que las sumas, restas, multiplicaciones y divisiones varían:
- Suma: esta operación en binario implica las siguientes operaciones bit a bit:
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 0 + 1 |
Por ejemplo, sumar 110 + 100 = 1010. Es decir, comenzando de derecha a izquierda, 0+0=0, 1+0=1 y 1+1=2 (pero como en binario no existe el 2, sino que es 10, sería 0 y te llevas 1).
- Resta: la resta binaria también es un tanto característica en este caso, coom puedes ver en la siguiente tabla:
| 0 | 0 | 0 |
| 1 | 0 | 1 (0-1 no esta permitido al dar negativo) |
| 1 | 1 | 0 |
Por ejemplo, 0-0=0, 1-0=0, 1-1=0, 101-010=11. Además, deberías saber que también se puede restar un binario usando complemento a dos. Sumando al minuendo el complemento a dos del sustraendo dará el resultado también.
Cuando se habla de un decimal con magnitud y signo se refiere a que se están representando números negativos. Para ello, se puede usar un 0 delante para signo positivo, y 1 para determinar que es negativo. Por ejemplo, si tenemos el valor 11 (3) y lo queremos representar con signo, podríamos usar 011 (+3) para el positivo y 111 (-3) para el negativo, pero indicándolo, ya que de lo contrario podría confundirse con el número 111 binario, que equivale a +7.
- Multiplicación: en cuanto a la multiplicación en binario, es bastante fácil, puesto que no tendrás que tener en cuenta tablas de multiplicar diferentes, solo los resultados con 0 y 1:
| 0 | 0 | 0 |
| 0 | 1 | 0 (igual para 1×0) |
| 1 | 1 | 1 |
Por tanto, lo único que daría como resultado un 1 sería la multiplicación de 1×1. Todas las demás configuraciones dan 0. Por ejemplo, 12×2 en binario sería 1100×10:
1100 x 10 = 11000
Si convertimos 11000 en decimal, vemos que realmente es un 24…
- División: en cuanto a la división, también es sencilla, y se puede entender como una multiplicación binaria y una resta binaria. Es decir, es igual que en la división decimal, pero a la hora de hacer las restas que haces en la división decimal, tienes que hacerlo como hemos visto en el punto de la resta. Y la multiplicación también como en el apartado de la multiplicación.
Para más información sobre las operaciones lógicas binarias, aquí tienes este otro artículo.
Coma flotante

Mientras que los números enteros son precisos, en los números de coma flotante (floating point o fixed point), no es así. Estos números representan fracciones o decimales, por lo que son más complejos. Además, para su representación hará falta algo más complejo que los simples bits de los enteros, como veremos.
Por ejemplo, almacenar en una memoria el número 2 (10) es tan fácil como almacenar los bits 10. Pero los números de coma flotante no se pueden almacenar igual, ya que tienes un problema ¿cuál es el primer número o valor que almacenas? Imagina 0.01. En este caso hay que definir cómo se debe almacenar de forma concreta.
Y es por eso que los números en coma flotante se dividen en tres componentes esenciales:
- Signo: es el signo positivo o negativo representado por un bit. Por ejemplo, 0 para los positivos y 1 para los negativos.
- Exponente: es el número que multiplica, y que se puede representar, por ejemplo, con 8-bits.
- Matisa: es el valor del número en sí, y se puede representar con 23-bits. Es decir, en total se suman 32-bit de longitud, aunque podrían tener longitudes diferentes como más adelante veremos.
Por ejemplo, un número binario en coma flotante sería:
10000000000000101010011110001000
En este caso tenemos el bit de signo, que es el 1, seguido de los byte que representa el exponente 00000000, y por último la matisa que es 00000101010011110001000.
Precisión
También hay que conocer qué es eso de la precisión de los valores de coma flotante, puesto que es algo que escucharás mucho cuando se trata de CPUs y GPUs y de pruebas de rendimiento para este tipo de datos.
- Precisión simple: se denominan así a los números de coma flotante que tienen 32-bits en total. En este caso se usan 4 bytes o 32-bit para representar el número, lo que daría como resultado algo no un número de 32 bits como se haría con los enteros, sino que habría que restar 1 bit para el signo, y otros 8 bits para el exponente, dejando 23 para la matisa como vimos antes.

- Precisión doble: se trata de números de 64-bit de longitud, es decir, permitirían representar mayor cantidad de valores que los de precisión simple. Por ejemplo, tenemos este caso, donde tenemos 1 bit de signo, 11 bit para el exponente, y 52 bits para la matisa:
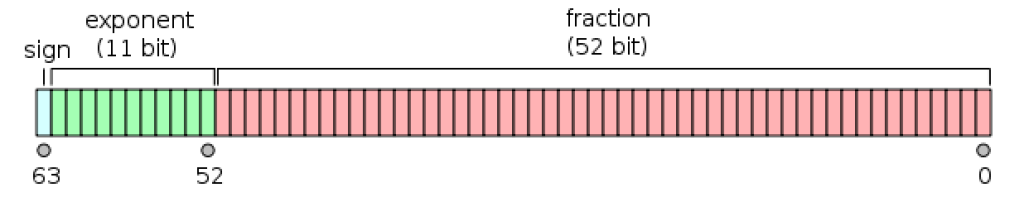
Aunque generalmente solo se habla de coma flotante de precisión simple y doble, también existen otros formatos, como los de 16-bit, los de 128-bit, etc. Aunque los más típicos son estos.
Desbordamiento

El desbordamiento (overflow, overrun) de coma flotante se produce cuando se intenta almacenar un número que es mayor que el que puede almacenar adecuadamente el modelo elegido. Esto generará errores, como deberías saber, ya que no todos los bits se pueden almacenar y el resultado de cualquier operación aritmética o lógica sería diferente al resultado real que se busca. Y esto generará un error de software…
Estándar IEEE 754
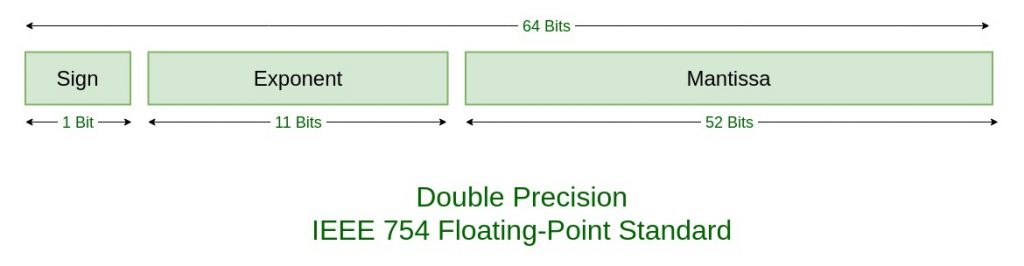
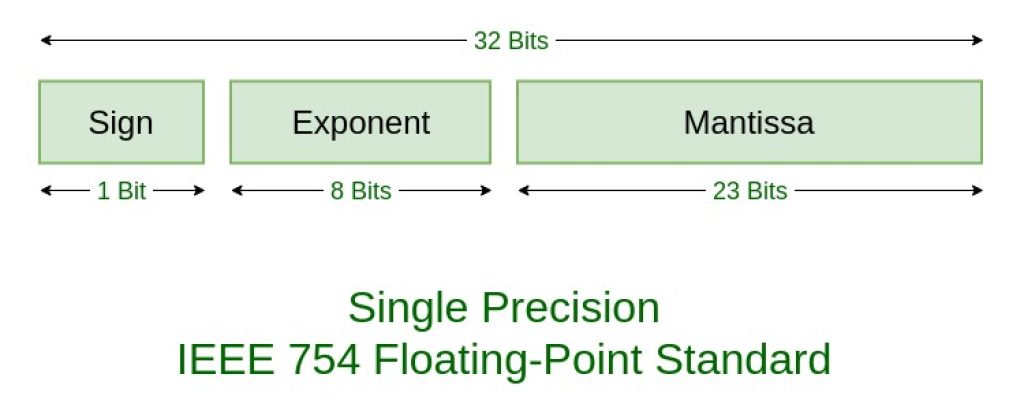
El estándar IEEE para aritmética de coma flotante (IEEE 754) es un estándar técnico para el cálculo de punto flotante que fue establecido en 1985 por el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE).
El estándar abordó muchos problemas encontrados en las diversas implementaciones de coma flotante que dificultaban su uso de forma fiable. Por eso, aunque puede haber otras representaciones más exóticas, hay que decir que el estándar IEEE 754 es la representación más común hoy en día para números reales en ordenadores, independientemente de la arquitectura de CPU usada y del sistema operativo.
Como ya dijimos anteriormente, el estándar IEEE 754 se compone de tres partes esenciales, pero estas partes tienen una longitud particular:
- Signo de la matisa: representa si se trata de un número positivo o un número negativo. Para los positivos se usa el bit 0, mientras que para los negativos se emplea el bit 1.
- Exponente sesgado: en este caso, se debe representar tanto de forma positiva como negativa. Se agrega un sesgo al exponente real para obtener el exponente almacenado.
- Matisa normalizada: en este caso es la base de un número en notación científica.
Por ejemplo, aquí tenemos los números IEEE 754 se dividen en dos según los tres componentes anteriores: precisión simple y precisión doble.
| TIPOS | SIGNO | EXPONENTE SESGADO | MANTISA NORMALIZADA | INCLINACIÓN |
|---|---|---|---|---|
| Precisión simple | 1 (bit 31) | 8(30-23) | 23(22-0) | 127 |
| Precisión doble | 1 (bit 63) | 11(62-52) | 52(51-0) | 1023 |
Ejemplo –
Ejemplo: 85.125
85 = 1010101
0,125 = 001
85,125 = 1010101,001
=1.010101001x2^6
signo = 0
Valores especiales
IEEE ha reservado algunos valores que pueden generar ambigüedad, y que son también muy importantes para que los conozcas:
- Cero: es un valor especial indicado con un exponente y una matisa de 0. En cambio, -0 y +0 son valores distintos, aunque ambos son iguales.
- Desnormalizado: si el exponente es todo ceros, pero la mantisa no, entonces el valor es un número desnormalizado. Esto significa que este número no tiene un número inicial asumido antes del punto binario.
- Infinito: los valores +infinito y -infinito se representan con un exponente con todos los bits del exponente a 1 y una mantisa de todo ceros. El bit de signo distingue entre infinito negativo e infinito positivo. Las operaciones con valores infinitos están bien definidas en IEEE.
- No es un número (NAN): el valor NAN se usa para representar un valor que es un error. Esto se representa cuando el campo del exponente son todos unos con un bit de signo cero o una mantisa que no es 1 seguida de ceros. Este es un valor especial que podría usarse para denotar una variable que aún no tiene un valor en la programación.
| EXPONENTE | mantisa | VALOR |
|---|---|---|
| 0 | 0 | exacto 0 |
| 255 | 0 | Infinidad |
| 0 | no 0 | desnormalizado |
| 255 | no 0 | No es un número (NAN) |
Similar para la precisión doble, pero en la tabla anterior, en vez de 255 habría que reemplazarlo por el valor 2049.
| Desnormalizado | Normalizado | Decimal aproximado | |
|---|---|---|---|
| Precisión simple | ± 2 -149 a (1 – 2 -23 )×2 -126 | ± 2 -126 a (2 – 2 -23 )×2 127 | ± aproximadamente 10 -44,85 a aproximadamente 10 38,53 |
| Precisión doble | ± 2 -1074 a (1 – 2 -52 )×2 -1022 | ± 2 -1022 a (2 – 2 -52 )×2 1023 | ± aproximadamente 10 -323,3 a aproximadamente 10 308,3 |
El rango de números de coma flotante positivos se puede dividir en números normalizados y números desnormalizados que usan solo una parte de la precisión de las fracciones. Dado que cada número de punto flotante tiene un valor negativo correspondiente, los rangos anteriores son simétricos alrededor de cero.
Hay cinco rangos numéricos distintos que los números de coma flotante de precisión simple no pueden representar con el esquema presentado hasta ahora:
- Números negativos menores que – (2 – 2 -23 ) × 2 127 (desbordamiento negativo)
- Números negativos mayores que – 2 -149 (desbordamiento negativo)
- Cero
- Números positivos menores que 2 -149 (subdesbordamiento positivo)
- Números positivos mayores que (2 – 2 -23 ) × 2 127 (desbordamiento positivo)
El desbordamiento generalmente significa que los valores han crecido demasiado para ser representados, como ya informé en el caso de los enteros. El subdesbordamiento es un problema menos grave porque solo denota una pérdida de precisión, que se garantiza que se aproximará mucho a cero.
A continuación se muestra la tabla del rango efectivo total de números finitos de coma flotante IEEE:
| Binario | Decimal | |
|---|---|---|
| Soltero | ± (2 – 2 -23 ) × 2 127 | aproximadamente ± 10 38,53 |
| Doble | ± (2 – 2 -52 ) × 2 1023 | aproximadamente ± 10 308,25 |
Operaciones Especiales
| Operación | Resultado |
|---|---|
| n ÷ ±Infinito | 0 |
| ±Infinito × ±Infinito | ±Infinito |
| ±distinto de cero ÷ ±0 | ±Infinito |
| ±finito × ±Infinito | ±Infinito |
| Infinito + Infinito Infinito – -Infinito | +Infinito |
| -Infinito – Infinito -Infinito + – Infinito | -Infinito |
| ±0 ÷ ±0 | NaN |
| ±Infinito ÷ ±Infinito | NaN |
| ±Infinito × 0 | Nan |
| NaN == NaN | False |
Como ves, los números en coma flotante son aún más complicados que los enteros, pero son muy necesarios para la computación actual.
Velocidad entero vs coma flotante

Es muy probable que estés pensado si es mejor un procesador con mayor rendimiento en enteros o con mayor rendimiento en coma flotante. Esto era algo muy frecuente en el pasado, ahora ha pasado a un segundo plano, pero aún es una pregunta interesante. Y es que el rendimiento del software dependerá de ello.
Generalmente, hay que decir que muchas de las aplicaciones convencionales que usas hacen uso más intensivo de operaciones con enteros. En cambio, cuando se trata de software científico o videojuegos, multimedia, etc., es ahí donde cobra mayor importancia el coma flotante. Por tanto, dependerá un poco del software que uses más frecuentemente.
En la actualidad tenemos la unidad FLOPS para describir el rendimiento de una máquina con los cálculos en coma flotante por segundo que puede desarrollar. Sin embargo, esta unidad es más eficaz para la supercomputación o HPC que para la computación doméstica.
Además, debes saber que se puede convertir entre unos y otros se se quisiese, aunque este es otro tema que no voy a desarrollar aquí.
También debes tener en cuenta que las instrucciones que trabajan con números enteros suelen tardar menos en procesarse, mientras que las de coma flotante podrían llevar más ciclos en terminar de calcularse. Por este motivo, no es tan fácil hacer una comparativa entre la cantidad de instrucciones por ciclo en enteros y en coma flotante.
